#include "jmodes.h"

Detailed Description

See also: jconfident for encryption algorithms

Block Modes of Operation

See https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation

In cryptography, a mode of operation is an algorithm that uses a block cipher to encrypt messages of arbitrary length in a way that provides confidentiality or authenticity. A block cipher by itself is only suitable for the secure cryptographic transformation (encryption or decryption) of one fixed-length group of bits called a block. A mode of operation describes how to repeatedly apply a cipher's single-block operation to securely transform amounts of data larger than a block

Most modes require a unique binary sequence, often called an initialization vector (IV), for each encryption operation. The IV has to be non-repeating and, for some modes, random as well. The initialization vector is used to ensure distinct ciphertexts are produced even when the same plaintext is encrypted multiple times independently with the same key.[6] Block ciphers have one or more block size(s), but during transformation the block size is always fixed. Block cipher modes operate on whole blocks and require that the last part of the data be padded to a full block if it is smaller than the current block size. There are, however, modes that do not require padding because they effectively use a block cipher as a stream cipher; such ciphers are capable of encrypting arbitrarily long sequences of bytes or bits

Historically, encryption modes have been studied extensively in regard to their error propagation properties under various scenarios of data modification. Later development regarded integrity protection as an entirely separate cryptographic goal. Some modern modes of operation combine confidentiality and authenticity in an efficient way, and are known as authenticated encryption modes

History and standardization

The earliest modes of operation, ECB, CBC, OFB, and CFB (see below for all), date back to 1981 and were specified in FIPS 81, DES modes of Operation. In 2001, the US National Institute of Standards and Technology (NIST) revised its list of approved modes of operation by including AES as a block cipher and adding CTR mode in SP800-38A, Recommendation for Block Cipher modes of Operation. Finally, in January, 2010, NIST added XTS-AES in SP800-38E, Recommendation for Block Cipher modes of Operation: The XTS-AES Mode for Confidentiality on Storage Devices. Other confidentiality modes exist which have not been approved by NIST. For example, CTS is ciphertext stealing mode and available in many popular cryptographic libraries

The block cipher modes ECB, CBC, OFB, CFB, CTR, and XTS provide confidentiality, but they do not protect against accidental modification or malicious tampering. Modification or tampering can be detected with a separate message authentication code such as CBC-MAC, or a digital signature. The cryptographic community recognized the need for dedicated integrity assurances and NIST responded with HMAC, CMAC, and GMAC. HMAC was approved in 2002 as FIPS 198, The Keyed-Hash Message Authentication Code (HMAC), CMAC was released in 2005 under SP800-38B, Recommendation for Block Cipher modes of Operation: The CMAC Mode for Authentication, and GMAC was formalized in 2007 under SP800-38D, Recommendation for Block Cipher modes of Operation: Galois/Counter Mode (GCM) and GMAC

After observing that compositing a confidentiality mode with an authenticity mode could be difficult and error prone, the cryptographic community began to supply modes which combined confidentiality and data integrity into a single cryptographic primitive. The modes are referred to as authenticated encryption, AE or "authenc". Examples of AE modes are CCM (SP800-38C), GCM (SP800-38D), CWC, EAX, IAPM, and OCB

modes of operation are nowadays defined by a number of national and internationally recognized standards bodies. Notable standards organizations include NIST, ISO (with ISO/IEC 10116), the IEC, the IEEE, the national ANSI, and the IETF

Initialization vector (IV)

An initialization vector (IV) or starting variable (SV) is a block of bits that is used by several modes to randomize the encryption and hence to produce distinct ciphertexts even if the same plaintext is encrypted multiple times, without the need for a slower re-keying process

An initialization vector has different security requirements than a key, so the IV usually does not need to be secret. However, in most cases, it is important that an initialization vector is never reused under the same key. For CBC and CFB, reusing an IV leaks some information about the first block of plaintext, and about any common prefix shared by the two messages. For OFB and CTR, reusing an IV completely destroys security. This can be seen because both modes effectively create a bitstream that is XORed with the plaintext, and this bitstream is dependent on the password and IV only. Reusing a bitstream destroys security. In CBC mode, the IV must, in addition, be unpredictable at encryption time; in particular, the (previously) common practice of re-using the last ciphertext block of a message as the IV for the next message is insecure (for example, this method was used by SSL 2.0). If an attacker knows the IV (or the previous block of ciphert(m_sec->get_field<direction_t>(field_t::DIRECTION)==direction_t::ENC)ext) before he specifies the next plaintext, he can check his guess about plaintext of some block that was encrypted with the same key before (this is known as the TLS CBC IV attack)

Padding

A block cipher works on units of a fixed size (known as a block size), but messages come in a variety of lengths. So some modes (namely ECB and CBC) require that the final block be padded before encryption. Several padding schemes exist. The simplest is to add null bytes to the plaintext to bring its length up to a multiple of the block size, but care must be taken that the original length of the plaintext can be recovered; this is trivial, for example, if the plaintext is a C style string which contains no null bytes except at the end. Slightly more complex is the original DES method, which is to add a single one bit, followed by enough zero bits to fill out the block; if the message ends on a block boundary, a whole padding block will be added. Most sophisticated are CBC-specific schemes such as ciphertext stealing or residual block termination, which do not cause any extra ciphertext, at the expense of some additional complexity. Schneier and Ferguson suggest two possibilities, both simple: append a byte with value 128 (hex 80), followed by as many zero bytes as needed to fill the last block, or pad the last block with n bytes all with value n

CFB, OFB and CTR modes do not require any special measures to handle messages whose lengths are not multiples of the block size, since the modes work by XORing the plaintext with the output of the block cipher. The last partial block of plaintext is XORed with the first few bytes of the last keystream block, producing a final ciphertext block that is the same size as the final partial plaintext block. This characteristic of stream ciphers makes them suitable for applications that require the encrypted ciphertext data to be the same size as the original plaintext data, and for applications that transmit data in streaming form where it is inconvenient to add padding bytes

Common modes(m_sec->get_field<direction_t>(field_t::DIRECTION)==direction_t::ENC)

Many modes of operation have been defined. Some of these are described below

Electronic Codebook (ECB)

The simplest of the encryption modes is the Electronic Codebook (ECB) mode. The message is divided into blocks, and each block is encrypted separately

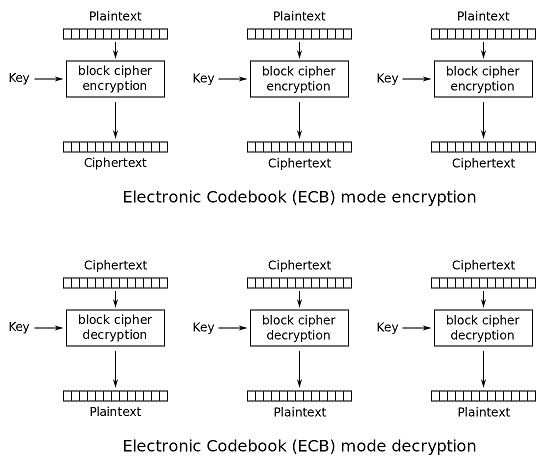
Electronic Code Book (ECB) Encryption Mode

The disadvantage of this method is that identical plaintext blocks are encrypted into identical ciphertext blocks; thus, it does not hide data patterns well. In some senses, it doesn't provide serious message confidentiality, and it is not recommended for use in cryptographic protocols at all

A striking example of the degree to which ECB can leave plaintext data patterns in the ciphertext can be seen when ECB mode is used to encrypt a bitmap image which uses large areas of uniform colour. While the colour of each individual pixel is encrypted, the overall image may still be discerned as the pattern of identically coloured pixels in the original remains in the encrypted version

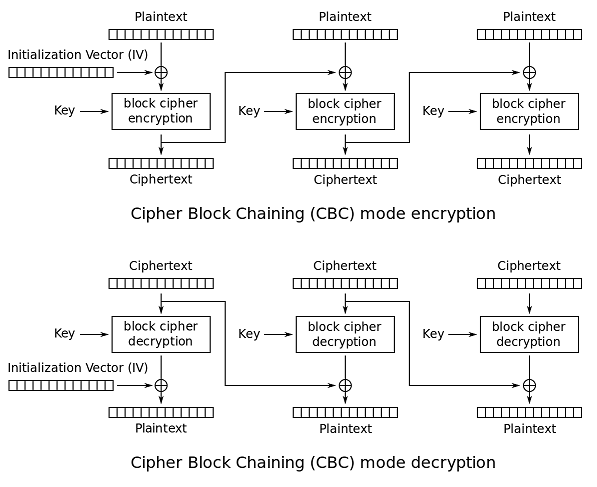
Cipher Block Chaining (CBC)

Ehrsam, Meyer, Smith and Tuchman invented the Cipher Block Chaining (CBC) mode of operation in 1976. In CBC mode, each block of plaintext is XORed with the previous ciphertext block before being encrypted. This way, each ciphertext block depends on all plaintext blocks processed up to that point. To make each message unique, an initialization vector must be used in the first block

Cipher Block Chaining (CBC) Encryption Mode

If the first block has index 1, the mathematical formula for CBC encryption is

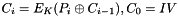
${C}_{i}={E}_{K}(P_{i}\oplus C_{i-1}),C_{0}=IV$

while the mathematical formula for CBC decryption is

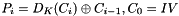
$P_{i}=D_{K}(C_{i})\oplus C_{i-1},C_{0}=IV$

CBC has been the most commonly used mode of operation. Its main drawbacks are that encryption is sequential (i.e., it cannot be parallelized), and that the message must be padded to a multiple of the cipher block size. One way to handle this last issue is through the method known as ciphertext stealing. Note that a one-bit change in a plaintext or IV affects all following ciphertext blocks

Decrypting with the incorrect IV causes the first block of plaintext to be corrupt but subsequent plaintext blocks will be correct. This is because each block is XORed with the ciphertext of the previous block, not the plaintext, so one does not need to decrypt the previous block before using it as the IV for the decryption of the current one. This means that a plaintext block can be recovered from two adjacent blocks of ciphertext. As a consequence, decryption can be parallelized. Note that a one-bit change to the ciphertext causes complete corruption of the corresponding block of plaintext, and inverts the corresponding bit in the following block of plaintext, but the rest of the blocks remain intact. This peculiarity is exploited in different padding oracle attacks, such as POODLE

Explicit Initialization Vectors takes advantage of this property by prepending a single random block to the plaintext. Encryption is done as normal, except the IV does not need to be communicated to the decryption routine. Whatever IV decryption uses, only the random block is "corrupted". It can be safely discarded and the rest of the decryption is the original plaintext

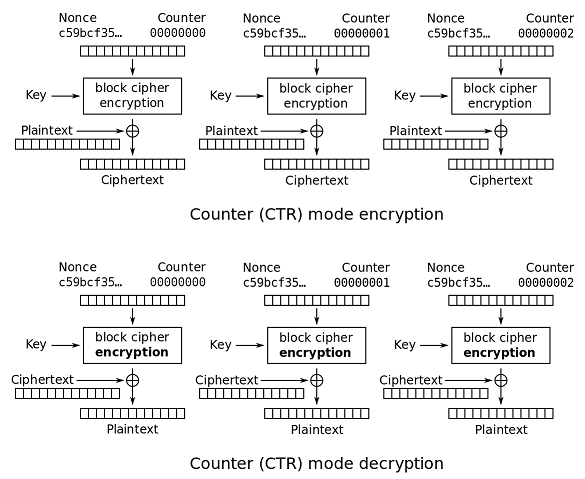
Counter (CTR)

Like OFB, Counter mode turns a block cipher into a stream cipher. It generates the next keystream block by encrypting successive values of a "counter". The counter can be any function which produces a sequence which is guaranteed not to repeat for a long time, although an actual increment-by-one counter is the simplest and most popular. The usage of a simple deterministic input function used to be controversial; critics argued that "deliberately exposing a cryptosystem to a known systematic input represents an unnecessary risk." However, today CTR mode is widely accepted and any problems are considered a weakness of the underlying block cipher, which is expected to be secure regardless of systemic bias in its input. Along with CBC, CTR mode is one of two block cipher jmodes recommended by Niels Ferguson and Bruce Schneier

CTR mode was introduced by Whitfield Diffie and Martin Hellman in 1979

CTR mode has similar characteristics to OFB, but also allows a random access property during decryption. CTR mode is well suited to operate on a multi-processor machine where blocks can be encrypted in parallel. Furthermore, it does not suffer from the short-cycle problem that can affect OFB

If the IV/nonce is random, then they can be combined together with the counter using any lossless operation (concatenation, addition, or XOR) to produce the actual unique counter block for encryption. In case of a non-random nonce (such as a packet counter), the nonce and counter should be concatenated (e.g., storing the nonce in the upper 64 bits and the counter in the lower 64 bits of a 128-bit counter block). Simply adding or XORing the nonce and counter into a single value would break the security under a chosen-plaintext attack in many cases, since the attacker may be able to manipulate the entire IV-counter pair to cause a collision. Once an attacker controls the IV-counter pair and plaintext, XOR of the ciphertext with the known plaintext would yield a value that, when XORed with the ciphertext of the other block sharing the same IV-counter pair, would decrypt that block

Note that the nonce in this diagram is equivalent to the initialization vector (IV) in the other diagrams. However, if the offset/location information is corrupt, it will be impossible to partially recover such data due to the dependence on byte offset

Counter Mode (CTR) Encryption Mode

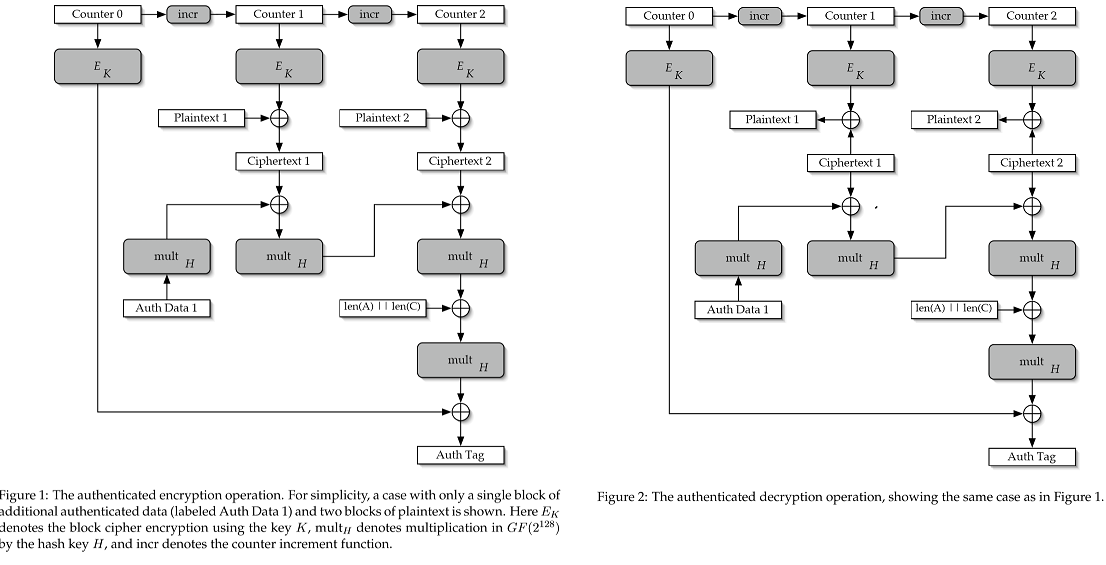
Galois Counter Mode (GCM)

Galois/Counter Mode (GCM) is a mode of operation for symmetric key cryptographic block ciphers that has been widely adopted because of its efficiency and performance. GCM throughput rates for state of the art, high speed communication channels can be achieved with reasonable hardware resources. The operation is an authenticated encryption algorithm designed to provide both data authenticity (integrity) and confidentiality. GCM is defined for block ciphers with a block size of 128 bits. Galois Message Authentication Code (GMAC) is an authentication-only variant of the GCM which can be used as an incremental message authentication code. Both GCM and GMAC can accept initialization vectors of arbitrary length

Different block cipher modes of operation can have significantly different performance and efficiency characteristics, even when used with the same block cipher. GCM can take full advantage of parallel processing and implementing GCM can make efficient use of an instruction pipeline or a hardware pipeline. In contrast, the cipher block chaining (CBC) mode of operation incurs significant pipeline stalls that hamper its efficiency and performance

Basic operation

In the normal counter mode, blocks are numbered sequentially, and then this block number is encrypted with a block cipher E, usually AES. The result of this encryption is then xored with the plain text to produce a cipher text. Like all counter modes, this is essentially a stream cipher, and so it is essential that a different initialization vector is used for each stream that is encrypted

The Galois Mult function then combines the ciphertext with an authentication code in order to produce an authentication tag that can be used to verify the integrity of the data. The encrypted text then contains the IV, cipher text, and authentication code. It therefore has similar security properties to a HMAC

Galios Field Counter Mode (GCM) Encryption Mode

Mathematical basis

GCM combines the well-known counter mode of encryption with the new Galois mode of authentication. The key feature is that the Galois field multiplication used for authentication can be easily computed in parallel. This option permits higher throughput than the authentication algorithms, like CBC, that use chaining modes. The 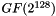$GF({2}^{128})$ field used is defined by the polynomial

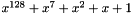
${x}^{128}+{x}^{7}+{x}^{2}+x+1$

The authentication tag is constructed by feeding blocks of data into the GHASH function and encrypting the result. This GHASH function is defined by

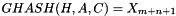
$GHASH(H,A,C)=X_{m+n+1}$

where H is the Hash Key, a string of 128 zero bits encrypted using the block cipher, A is data which is only authenticated (not encrypted), C is the ciphertext, m is the number of 128 bit blocks in A, n is the number of 128 bit blocks in C (the final blocks of A and C need not be exactly 128 bits), and the variable 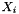$X_{i}$ for i = 0, ..., m + n + 1 is defined as

GCM Mathematical Computation

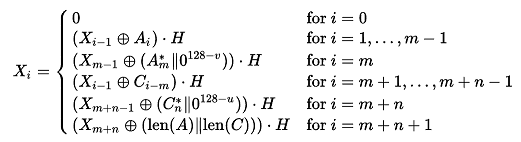
where v is the bit length of the final block of A, u is the bit length of the final block of 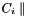$C_{i} \parallel$ denotes concatenation of bit strings, and len(A) and len(C) are the 64-bit representations of the bit lengths of A and C, respectively. Note that this is an iterative algorithm: each $X_{i}$ depends on $X_{i−1}$ and only the final $X_{i}$ is retained as output

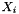
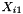
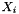
GCM mode was designed by John Viega and David A. McGrew as an improvement to Carter–Wegman Counter CWC mode

In November 2007, NIST announced the release of NIST Special Publication 800-38D Recommendation for Block Cipher modes of Operation: Galois/Counter Mode (GCM) and GMAC making GCM and GMAC official standards

Use

GCM mode is used in the IEEE 802.1AE (MACsec) Ethernet security, IEEE 802.11ad (also known as WiGig), ANSI (INCITS) Fibre Channel Security Protocols (FC-SP), IEEE P1619.1 tape storage, IETF IPsec standards, SSH and TLS 1.2. AES-GCM is included in the NSA Suite B Cryptography

Performance

GCM is ideal for protecting packetized data because it has minimum latency and minimum operation overhead

GCM requires one block cipher operation and one 128-bit multiplication in the Galois field per each block (128 bit) of encrypted and authenticated data. The block cipher operations are easily pipelined or parallelized; the multiplication operations are easily pipelined and can be parallelized with some modest effort (either by parallelizing the actual operation, by adapting Horner's method as described in the original NIST submission, or both)

Intel has added the PCLMULQDQ instruction, highlighting its use for GCM. This instruction enables fast multiplication over GF(2n), and can be used with any field representation

Impressive performance results have been published for GCM on a number of platforms. Käsper and Schwabe described a "Faster and Timing-Attack Resistant AES-GCM" that achieves 10.68 cycles per byte AES-GCM authenticated encryption on 64-bit Intel processors. Dai et al. report 3.5 cycles per byte for the same algorithm when using Intel's AES-NI and PCLMULQDQ instructions. Shay Gueron and Vlad Krasnov achieved 2.47 cycles per byte on the 3rd generation Intel processors. Appropriate patches were prepared for the OpenSSL and NSS libraries

When both authentication and encryption need to be performed on a message, a software implementation can achieve speed gains by overlapping the execution of those operations. Performance is increased by exploiting instruction level parallelism by interleaving operations. This process is called function stitching, and while in principle it can be applied to any combination of cryptographic algorithms, GCM is especially suitable. Manley and Gregg show the ease of optimizing when using function-stitching with GCM. They present a program generator that takes an annotated C version of a cryptographic algorithm and generates code that runs well on the target processor

Counter with CBC-MAC (CCM)

CCM mode (Counter with CBC-MAC) is a mode of operation for cryptographic block ciphers. It is an authenticated encryption algorithm designed to provide both authentication and confidentiality. CCM mode is only defined for block ciphers with a block length of 128 bits. In RFC 3610, it is defined for use with AES

The Initialization Vector (IV) of CCM must be carefully chosen to never be used more than once for a given key. This is because CCM is a derivation of CTR mode and the latter is effectively a stream cipher

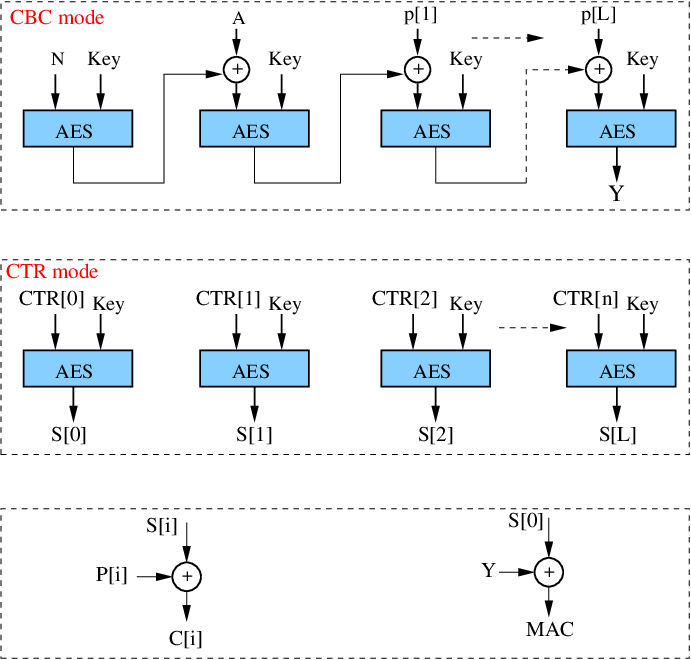
AES Counter with CBC-MAC (CCM) Encryption Mode

Encryption and authentication

As the name suggests, CCM mode combines the well known CBC-MAC with the well known counter mode of encryption. These two primitives are applied in an "authenticate-then-encrypt" manner, that is, CBC-MAC is first computed on the message to obtain a tag t; the message and the tag are then encrypted using counter mode. One key insight is that the same encryption key can be used for both, provided that the counter values used in the encryption do not collide with the (pre-)initialization vector used in the authentication. A proof of security exists for this combination, based on the security of the underlying block cipher. The proof also applies to a generalization of CCM for any size block cipher, and for any size cryptographically strong pseudo-random function (since in both counter mode and CBC-MAC, the block cipher is only ever used in one direction)

CCM mode was designed by Russ Housley, Doug Whiting and Niels Ferguson. At the time CCM mode was developed, Russ Housley was employed by RSA Laboratories

A minor variation of the CCM, called CCM*, is used in the ZigBee standard. CCM* includes all of the features of CCM and additionally offers encryption-only and integrity-only capabilities

Performance

CCM requires two block cipher encryption operations per each block of an encrypted-and-authenticated message, and one encryption per each block of associated authenticated data

According to Crypto++ benchmarks, AES CCM requires 28.6 cycles per byte on an Intel Core 2 processor in 32-bit mode

XEX-based tweaked-codebook mode with ciphertext stealing (XTS)

See https://en.wikipedia.org/wiki/Disk_encryption_theory#XTS

Ciphertext stealing provides support for sectors with size not divisible by block size, for example, 520-byte sectors and 16-byte blocks. XTS-AES was standardized on 2007-12-19[9] as IEEE P1619.[10] The standard supports using a different key for the IV encryption than for the block encryption; this is contrary to the intent of XEX and seems to be rooted in a misinterpretation of the original XEX paper, but does not harm security.[11][7] As a result, users wanting AES-256 and AES-128 encryption must supply 512 bits and 256 bits of key respectively

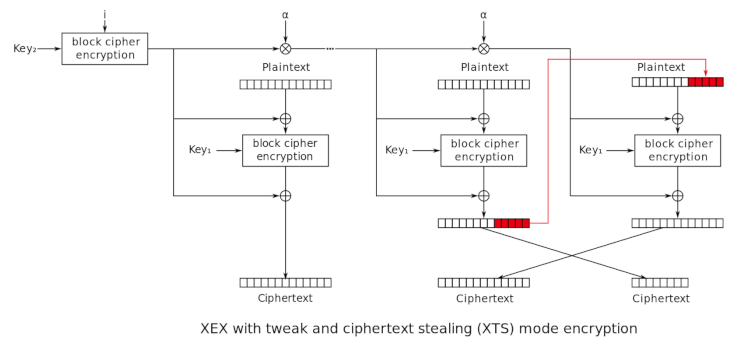
XEX-based tweaked-codebook with cipher-text stealing (XTS) Encryption Mode

On January 27, 2010, NIST released Special Publication (SP) 800-38E in final form. SP 800-38E is a recommendation for the XTS-AES mode of operation, as standardized by IEEE Std 1619-2007, for cryptographic modules. The publication approves the XTS-AES mode of the AES algorithm by reference to the IEEE Std 1619-2007, subject to one additional requirement, which limits the maximum size of each encrypted data unit (typically a sector or disk block) to 220 AES blocks According to SP 800-38E, "In the absence of authentication or access control, XTS-AES provides more protection than the other approved confidentiality-only modes against unauthorized manipulation of the encrypted data."

XTS weaknesses

XTS mode is susceptible to data manipulation and tampering, and applications must employ measures to detect modifications of data if manipulation and tampering is a concern: "...since there are no authentication tags then any ciphertext (original or modified by attacker) will be decrypted as some plaintext and there is no built-in mechanism to detect alterations. The best that can be done is to ensure that any alteration of the ciphertext will completely randomize the plaintext, and rely on the application that uses this transform to include sufficient redundancy in its plaintext to detect and discard such random plaintexts" This would require maintaining checksums for all data and metadata on disk, as done in ZFS or Btrfs. However, in commonly used file systems such as ext4 and NTFS only metadata is protected against tampering, while the detection of data tampering is non-existent

The mode is susceptible to traffic analysis, replay and randomization attacks on sectors and 16-byte blocks. As a given sector is rewritten, attackers can collect fine-grained (16 byte) ciphertexts, which can be used for analysis or replay attacks (at a 16-byte granularity). It would be possible to define sector-wide block ciphers, unfortunately with degraded performance

The AES-XCBC-MAC-96 Algorithm and Its Use With IPsec

A Message Authentication Code (MAC) is a key-dependent one way hash function. One popular way to construct a MAC algorithm is to use a block cipher in conjunction with the Cipher-Block-Chaining (CBC) mode of operation. The classic CBC-MAC algorithm, while secure for messages of a pre-selected fixed length, has been shown to be insecure across messages of varying lengths such as the type found in typical IP datagrams. This memo specifies the use of AES in CBC mode with a set of extensions to overcome this limitation. This new algorithm is named AES-XCBC-MAC-96

AES-XCBC-MAC-96

[AES] describes the underlying AES algorithm, while [CBC-MAC-1] and [XCBC-MAC-1] describe the AES-XCBC-MAC algorithm

The AES-XCBC-MAC-96 algorithm is a variant of the basic CBC-MAC with obligatory 10* padding; however, AES-XCBC-MAC-96 is secure for messages of arbitrary length. The AES-XCBC-MAC-96 calculations require numerous encryption operations; this encryption MUST be accomplished using AES with a 128-bit key. Given a 128-bit secret key K, AES-XCBC-MAC-96 is calculated as follows for a message M that consists of n blocks, M[1] ... M[n], in which the blocksize of blocks M[1] ... M[n-1] is 128 bits and the blocksize of block M[n] is between 1 and 128 bits:

Derive 3 128-bit keys (K1, K2 and K3) from the 128-bit secret key K, as follows:
- K1 = 0x01010101010101010101010101010101 encrypted with Key K
- K2 = 0x02020202020202020202020202020202 encrypted with Key K
- K3 = 0x03030303030303030303030303030303 encrypted with Key K
Define E[0] = 0x00000000000000000000000000000000
For each block M[i], where i = 1 ... n-1:
- XOR M[i] with E[i-1], then encrypt the result with Key K1, yielding E[i]
For block M[n]:

a. If the blocksize of M[n] is 128 bits:
- XOR M[n] with E[n-1] and Key K2, then encrypt the result with Key K1, yielding E[n]
b. If the blocksize of M[n] is less than 128 bits:
- Pad M[n] with a single "1" bit, followed by the number of "0" bits (possibly none) required to increase M[n]’s blocksize to 128 bits
- XOR M[n] with E[n-1] and Key K3, then encrypt the result with Key K1,yielding E[n]
The authenticator value is the leftmost 96 bits of the 128-bit E[n]

NOTE1: If M is the empty string, pad and encrypt as in (4)(b) to create M[1] and E[1]. This will never be the case for ESP or AH, but is included for completeness sake

NOTE2: [CBC-MAC-1] defines K1 as follows:

K1 = Constant1A encrypted with Key K | Constant1B encrypted with Key K

However, the second encryption operation is only needed for AES-XCBC-MAC with keys greater than 128 bits; thus, it is not included in the definition of AES-XCBC-MAC-96

AES-XCBC-MAC-96 verification is performed as follows:

Upon receipt of the AES-XCBC-MAC-96 authenticator, the entire 128-bit value is computed and the first 96 bits are compared to the value stored in the authenticator field.

Keying Material

AES-XCBC-MAC-96 is a secret key algorithm. For use with either ESP or AH a fixed key length of 128-bits MUST be supported. Key lengths other than 128-bits MUST NOT be supported (i.e., only 128-bit keys are to be used by AES-XCBC-MAC-96).

AES-XCBC-MAC-96 actually requires 384 bits of keying material (128 bits for the AES keysize + 2 times the blocksize). This keying material can either be provided through the key generation mechanism or it can be generated from a single 128-bit key. The latter approach has been selected for AES-XCBC-MAC-96, since it is analogous to other authenticators used within IPsec. The reason AES-XCBC-MAC-96 uses 3 keys is so the length of the input stream does not need to be known in advance. This may be useful for systems that do one-pass assembly of large packets

A strong pseudo-random function MUST be used to generate the required 128-bit key. This key, along with the 3 derived keys (K1, K2 and K3), should be used for no purposes other than those specified in the algorithm. In particular, they should not be used as keys in another cryptographic setting. Such abuses will invalidate the security of the authentication algorithm

At the time of this writing there are no specified weak keys for use with AES-XCBC-MAC-96. This does not mean to imply that weak keys do not exist. If, at some point, a set of weak keys for AES-XCBC-MAC-96 are identified, the use of these weak keys MUST be rejected followed by a request for replacement keys or a newly negotiated Security Association

[ARCH] describes the general mechanism for obtaining keying material when multiple keys are required for a single SA (e.g., when an ESP SA requires a key for confidentiality and a key for authentication)

In order to provide data origin authentication, the key distribution mechanism must ensure that unique keys are allocated and that they are distributed only to the parties participating in the communication

Current attacks do not necessitate a specific recommended frequency for key changes. However, periodic key refreshment is a fundamental security practice that helps against potential weaknesses of the function and the keys, reduces the information available to a cryptanalyst, and limits the damage resulting from a compromised key

Padding

AES-XCBC-MAC-96 operates on 128-bit blocks of data. Padding requirements are specified in [CBC-MAC-1] and are part of the XCBC algorithm. If you build AES-XCBC-MAC-96 according to [CBC-MAC-1] you do not need to add any additional padding as far as AES-XCBC-MAC-96 is concerned. With regard to "implicit packet padding" as defined in [AH], no implicit packet padding is required

Truncation

AES-XCBC-MAC produces a 128-bit authenticator value. AES-XCBC-MAC-96 is derived by truncating this 128-bit value as described in [HMAC] and verified in [XCBC-MAC-2]. For use with either ESP or AH, a truncated value using the first 96 bits MUST be supported. Upon sending, the truncated value is stored within the authenticator field. Upon receipt, the entire 128-bit value is computed and the first 96 bits are compared to the value stored in the authenticator field. No other authenticator value lengths are supported by AES-XCBC-MAC-96

The length of 96 bits was selected because it is the default authenticator length as specified in [AH] and meets the security requirements described in [XCBC-MAC-2]

Interaction with the ESP Cipher Mechanism

As of this writing, there are no known issues which preclude the use of AES-XCBC-MAC-96 with any specific cipher algorithm

Performance

For any CBC MAC variant, the major computational effort is expended in computing the underlying block cipher. This algorithm uses a minimum number of AES invocations, one for each block of the message or fraction thereof, resulting in performance equivalent to classic CBC-MAC. The key expansion requires 3 additional AES encryption operations, but these can be performed once in advance for each secret key

The CMAC Mode for Authentication

See NIST800-38b

Block Cipher

The CMAC algorithm depends on the choice of an underlying symmetric key block cipher. The CMAC algorithm is thus a mode of operation (a mode, for short) of the block cipher. The CMAC key is the block cipher key (the key, for short For any given key, the underlying block cipher of the mode consists of two functions that are inverses of each other. The choice of the block cipher includes the designation of one of the two functions of the block cipher as the forward function/transformation, and the other as the inverse function, as in the specifications of the AES algorithm and TDEA in Ref. [3] and Ref. [10], respectively. The CMAC mode does not employ the inverse function

The forward cipher function is a permutation on bit strings of a fixed length; the strings are called blocks. The bit length of a block is denoted b, and the length of a block is called the block size. For the AES algorithm, b = 128; for TDEA, b = 64. The key is denoted K, and the resulting forward cipher function of the block cipher is denoted 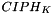${CIPH}_{K}$

The underlying block cipher shall be approved, and the key shall be generated uniformly at random, or close to uniformly at random, i.e., so that each possible key is (nearly) equally likely to be generated. The key shall be secret and shall be used exclusively for the CMAC mode of the chosen block cipher. The message span of the key is discussed in Appendix B. To fulfill the requirements on the key, the key should be established among the parties to the information within an approved key management structure; the details of the establishment and management of keys are outside the scope of this Recommendation

Subkeys

The block cipher key is used to derive two additional secret values, called the subkeys, denoted K1 and K2. The length of each subkey is the block size. The subkeys are fixed for any invocation of CMAC with the given key. Consequently, the subkeys may be precomputed and stored with the key for repeated use; alternatively, the subkeys may be computed anew for each invocation

Any intermediate value in the computation of the subkey, in particular, CIPHK(0b), shall also be secret. This requirement precludes the system in which CMAC is implemented from using this intermediate value publicly for some other purpose, for example, as an unpredictable value or as an integrity check value on the key. One of the elements of the subkey generation process is a bit string, denoted Rb, that is completely determined by the number of bits in a block. 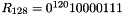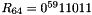In particular, for the two block sizes of the currently approved block ciphers, ${R}_{128} = {0}^{120}10000111$ , and ${R}_{64} = {0}^{59}11011$

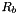
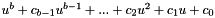
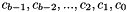
In general, ${R}_{b}$ is a representation of a certain irreducible binary polynomial of degree b, namely, the lexicographically first among all such polynomials with the minimum possible number of nonzero terms. 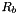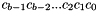If this polynomial is expressed as ${u}^{b}+{c}_{b-1}{u}^{b-1}+...+{c}_{2}{u}^{2}+{c}_{1}u+{c}_{0}$ , where the coefficients ${c}_{b-1}, {c}_{b-2}, ..., {c}_{2}, {c}_{1}, {c}_{0}$ are either 0 or 1, then ${R}_{b}$ is the bit string ${c}_{b-1}{c}_{b-2}...{c}_{2}{c}_{1}{c}_{0}$

MAC Generation and Verification

As for any MAC algorithm, an authorized party applies the MAC generation process to the data to be authenticated to produce a MAC for the data. Subsequently, any authorized party can apply the verification process to the received data and the received MAC. Successful verification provides assurance of data authenticity, as discussed in Appendix A, and, hence, of integrity

Input and Output Data

For a given block cipher and key, the input to the MAC generation function is a bit string called the message, denoted M. The bit length of M is denoted Mlen. The value of Mlen is not an essential input for the MAC generation algorithm if the implementation has some other means of identifying the last block in the partition of the message, as discussed in Sec. 6.2. Thus, in such a case, the computation of the MAC may begin “on-line” before the entire message is available. In principle, there is no restriction on the lengths of messages. In practice, however, the system in which CMAC is implemented may restrict the length of the input messages to the MAC generation function

The output of the MAC generation function is a bit string called the MAC, denoted T. The length of T, denoted Tlen, is a parameter that shall be fixed for all invocations of CMAC with the given key. The requirements for the selection of Tlen are given in Appendix A

CMAC Specification

Subkey generation, MAC generation, and MAC verification are specified in Sections 6.1, 6.2, and 6.3 below. The specifications include the inputs, the outputs, a suggested notation for the function, the steps, and a summary; for MAC generation, a diagram is also given. The inputs that are typically fixed across many invocations of CMAC are called the prerequisites. The prerequisites and the other inputs shall meet the requirements in Sec. 5. The suggested notation does not include the block cipher

Subkey Generation

The following is a specification of the subkey generation process of CMAC: Prerequisites:

block cipher CIPH with block size b
key K

Output:

subkeys K1, K2

Suggested Notation:

SUBK(K)

Steps:

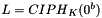
Let $L = {CIPH}_{K}({0}^{b})$
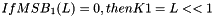
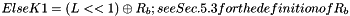
$If {MSB}_{1}(L) = 0, then K1 = L << 1$ ; $Else K1 = (L << 1) \oplus {R}_{b}; see Sec. 5.3 for the definition of {R}_{b}$
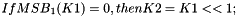
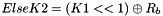
$If {MSB}_{1}(K1) = 0, then K2 = K1 << 1;$ $Else K2 = (K1 << 1) \oplus {R}_{b}$
Return K1, K2

In Step 1, the block cipher is applied to the block that consists entirely of ‘0’ bits. In Step 2, the first subkey is derived from the resulting string by a left shift of one bit, and, conditionally, by XORing a constant that depends on the block size. In Step 3, the second subkey is derived in the same manner from the first subkey.1 As discussed in Sec. 5.3, any intermediate value in the computation of the subkey, in particular, 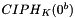${CIPH}_{K}({0}^{b})$ , shall be secret

MAC Generation

The following is a specification of the MAC generation process of CMAC: Prerequisites:

block cipher CIPH with block size b
key K
MAC length parameter Tlen

Input:

message M of bit length Mlen.

Output:

MAC T of bit length Tlen

Suggested Notation:

CMAC(K, M, Tlen) or, if Tlen is understood from the context, CMAC(K, M)

Steps:

Apply the subkey generation process in Sec. 6.1 to K to produce K1 and K2
If Mlen = 0, let n = 1; else, let n = [Mlen/blk_size]
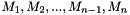
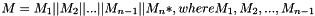
Let ${M}_{1}, {M}_{2}, ... , {M}_{n-1}, {M}_{n}$ denote the unique sequence of bit strings such that $M = {M}_{1} || {M}_{2} || ... || {M}_{n-1} || {M}_{n}*, where {M}_{1}, {M}_{2},...,{M}_{n-1}$ are complete blocks
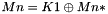
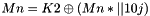
If Mn* is a complete block, let $Mn = K1 \oplus Mn*$ ; else, let $Mn = K2 \oplus (Mn*||10j)$ , where j = nb-Mlen-1
Let ${C}_{0} = {0}^{b}$
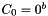
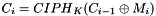
For i = 1 to n, let ${C}_{i} = {CIPH}_{K}({C}_{i-1}\oplus{M}_{i})$
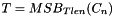
Let $T = {MSB}_{Tlen}({C}_{n})$
Return T

In Step 1, the subkeys are generated from the key. In Steps 2–4, the input message is formatted into a sequence of complete blocks in which the final block has been masked by a subkey. There are two cases:

If the message length is a positive multiple of the block size, then the message is partitioned into complete blocks. The final block is masked with the first subkey; in other words, the final block in the partition is replaced with the exclusive-OR of the final block with the first subkey. The resulting sequence of blocks is the formatted message
If the message length is not a positive multiple of the block size, then the message is partitioned into complete blocks to the greatest extent possible, i.e., into a sequence of complete blocks followed by a final bit string whose length is less than the block size. A padding string is appended to this final bit string, in particular, a single ‘1’ bit followed by the minimum number of ‘0’ bits, possibly none, that are necessary to form a complete block. The complete final block is masked, as described in the previous bullet, with the second subkey. The resulting sequence of blocks is the formatted message

In Steps 5 and 6, the cipher block chaining (CBC) technique, with the zero block as the initialization vector, is applied to the formatted message. In Steps 7 and 8, the final CBC output block is truncated according to the MAC length parameter that is associated with the key, and the result is returned as the MAC

Equivalent sets of steps, i.e., procedures that yield the correct output from the same input, are permitted. For example, it is not necessary to complete the formatting of the entire message (Steps 3 and 4) prior to the cipher block chaining (Steps 5 and 6). Instead, the iterations of Step 5 may be executed “on the fly,” i.e., on each successive block of the message as soon as it is available for processing. Step 4 may be delayed until the final bit string in the partition is available; the appropriate case, and value of j, if necessary, can be determined from the length of the final bit string. In such an implementation, the determination in Step 2 of the total number of blocks in the formatted message may be omitted, assuming that the implementation has another way to identify the final string in the partition.

Similarly, the subkeys need not be computed anew for each invocation of CMAC with a given key; instead, they may be precomputed and stored along with the key as algorithm inputs.

Counter Mode MAC Generation

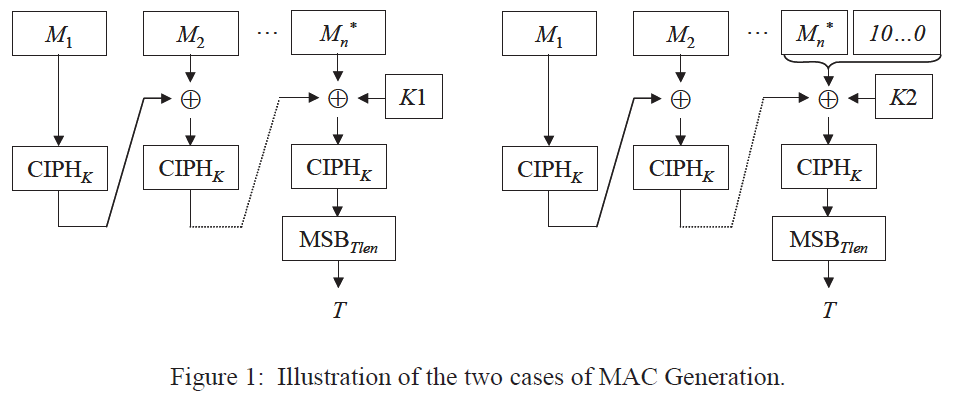
The two cases of MAC Generation are illustrated in Figure 1 above. On the left is the case where the message length is a positive multiple of the block size; on the right is the case where the message length is not a positive multiple of the block length

MAC Verification

The following is a specification of the MAC verification process of CMAC: Prerequisites:

block cipher CIPH with block size b
key K
subkeys K1, K2
MAC length Tlen

Input:

message M of bit length Mlen
received MAC T'

Output:

VALID or INVALID

Suggested Notation:

VER(K, M, T')

Steps:

Apply the MAC generation process in Sec. 6.2 to M to produce T
If T = T', return VALID; else, return INVALID

In Step 1, the MAC generation process in Sec. 6.2 is applied to the message, and, in Step 2, the resulting MAC is compared with the received MAC to determine its validity

For API Documentation:

See also: ProtocolPP::ciphers; ProtocolPP::jmodes; ProtocolPP::jsnow3g; ProtocolPP::jsnowv; ProtocolPP::jzuc

For Additional Documentation:

See also: ciphers; jmodes; jsnow3g; jsnowv; jzuc

The source code contained or described herein and all documents related to the source code (herein called "Material") are owned by John Peter Greninger and Sheila Rocha Greninger. Title to the Material remains with John Peter Greninger and Sheila Rocha Greninger. The Material contains trade secrets and proprietary and confidential information of John Peter Greninger and Sheila Rocha Greninger. The Material is protected by worldwide copyright and trade secret laws and treaty provisions. No part of the Material may be used, copied, reproduced, modified, published, uploaded, posted, transmitted, distributed, or disclosed in any way without prior express written consent of John Peter Greninger and Sheila Rocha Greninger (both are required)

No license under any patent, copyright, trade secret, or other intellectual property right is granted to or conferred upon you by disclosure or delivery of the Materials, either expressly, by implication, inducement, estoppel, or otherwise. Any license under such intellectual property rights must be express and approved by John Peter Greninger and Sheila Rocha Greninger in writing

Licensing information can be found at www.protocolpp.com/license with use of the binary forms permitted provided that the following conditions are met:

Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution
Any and all modifications must be returned to John Peter Greninger at GitHub.com https://github.com/jpgreninger/protocolpp for evaluation. Inclusion of modifications in the source code shall be determined solely by John Peter Greninger. Failure to provide modifications shall render this license NULL and VOID and revoke any rights to use of Protocol++®
Commercial use (incidental or not) requires a fee-based license obtainable at www.protocolpp.com/shop
Academic or research use requires prior written and notarized permission from John Peter and Sheila Rocha Greninger

Use of the source code requires purchase of the source code. Source code can be purchased at www.protocolpp.com/shop

US Copyrights at https://www.copyright.gov/
- TXu002059872 (Version 1.0.0)
- TXu002066632 (Version 1.2.7)
- TXu002082674 (Version 1.4.0)
- TXu002097880 (Version 2.0.0)
- TXu002169236 (Version 3.0.1)
- TXu002182417 (Version 4.0.0)
- TXu002219402 (Version 5.0.0)
- TXu002272076 (Version 5.2.1)
- TXu002383571 (Version 5.4.3)

The name of its contributor may not be used to endorse or promote products derived from this software without specific prior written permission and licensing

THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDER AND CONTRIBUTOR "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE

The documentation for this class was generated from the following file:

include/jmodes.h