jintegritysa Class Reference

#include "include/jintegritysa.h"

Detailed Description

MD5 Message-Digest Algorithm

See https://en.wikipedia.org/wiki/MD5

The MD5 message-digest algorithm is a widely used hash function producing a 128-bit hash value. Although MD5 was initially designed to be used as a cryptographic hash function, it has been found to suffer from extensive vulnerabilities. It can still be used as a checksum to verify data integrity, but only against unintentional corruption. It remains suitable for other non-cryptographic purposes, for example for determining the partition for a particular key in a partitioned database

MD5 was designed by Ronald Rivest in 1991 to replace an earlier hash function MD4,[4] and was specified in 1992 as RFC 1321

One basic requirement of any cryptographic hash function is that it should be computationally infeasible to find two distinct messages that hash to the same value. MD5 fails this requirement catastrophically; such collisions can be found in seconds on an ordinary home computer

The weaknesses of MD5 have been exploited in the field, most infamously by the Flame malware in 2012. The CMU Software Engineering Institute considers MD5 essentially "cryptographically broken and unsuitable for further use"

As of 2019, MD5 continues to be widely used, in spite of its well-documented weaknesses and deprecation by security experts

Security

The security of the MD5 hash function is severely compromised. A collision attack exists that can find collisions within seconds on a computer with a 2.6 GHz Pentium 4 processor (complexity of 224.1). Further, there is also a chosen-prefix collision attack that can produce a collision for two inputs with specified prefixes within seconds, using off-the-shelf computing hardware (complexity 239). The ability to find collisions has been greatly aided by the use of off-the-shelf GPUs. On an NVIDIA GeForce 8400GS graphics processor, 16–18 million hashes per second can be computed. An NVIDIA GeForce 8800 Ultra can calculate more than 200 million hashes per second

These hash and collision attacks have been demonstrated in the public in various situations, including colliding document files and digital certificates. As of 2015, MD5 was demonstrated to be still quite widely used, most notably by security research and antivirus companies

As of 2019, one quarter of widely used content management systems were reported to still use MD5 for password hashing

Applications

MD5 digests have been widely used in the software world to provide some assurance that a transferred file has arrived intact. For example, file servers often provide a pre-computed MD5 (known as md5sum) checksum for the files, so that a user can compare the checksum of the downloaded file to it. Most unix-based operating systems include MD5 sum utilities in their distribution packages; Windows users may use the included PowerShell function "Get-FileHash", install a Microsoft utility, or use third-party applications. Android ROMs also use this type of checksum.

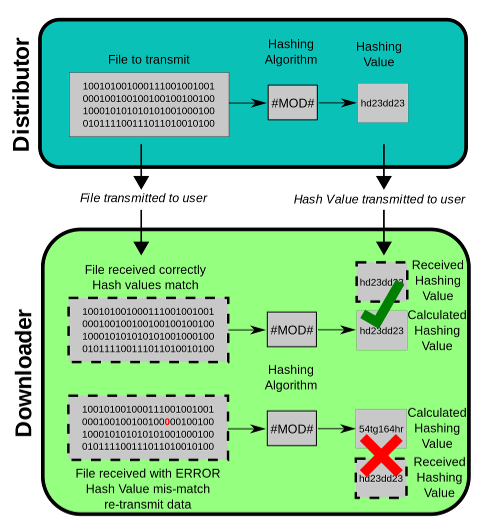
As it is easy to generate MD5 collisions, it is possible for the person who created the file to create a second file with the same checksum, so this technique cannot protect against some forms of malicious tampering. In some cases, the checksum cannot be trusted (for example, if it was obtained over the same channel as the downloaded file), in which case MD5 can only provide error-checking functionality: it will recognize a corrupt or incomplete download, which becomes more likely when downloading larger files

Historically, MD5 has been used to store a one-way hash of a password, often with key stretching. NIST does not include MD5 in their list of recommended hashes for password storage

MD5 is also used in the field of electronic discovery, in order to provide a unique identifier for each document that is exchanged during the legal discovery process. This method can be used to replace the Bates stamp numbering system that has been used for decades during the exchange of paper documents. As above, this usage should be discouraged due to the ease of collision attacks

Algorithm

MD5 processes a variable-length message into a fixed-length output of 128 bits. The input message is broken up into chunks of 512-bit blocks (sixteen 32-bit words); the message is padded so that its length is divisible by 512. The padding works as follows: first a single bit, 1, is appended to the end of the message. This is followed by as many zeros as are required to bring the length of the message up to 64 bits fewer than a multiple of 512. The remaining bits are filled up with 64 bits representing the length of the original message, modulo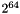

The main MD5 algorithm operates on a 128-bit state, divided into four 32-bit words, denoted A, B, C, and D. These are initialized to certain fixed constants. The main algorithm then uses each 512-bit message block in turn to modify the state. The processing of a message block consists of four similar stages, termed rounds; each round is composed of 16 similar operations based on a non-linear function F, modular addition, and left rotation. The figure below illustrates one operation within a round. There are four possible functions, a different one is used in each round:

denote the XOR, AND, OR and NOT operations respectively

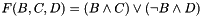
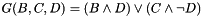
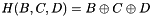
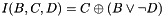
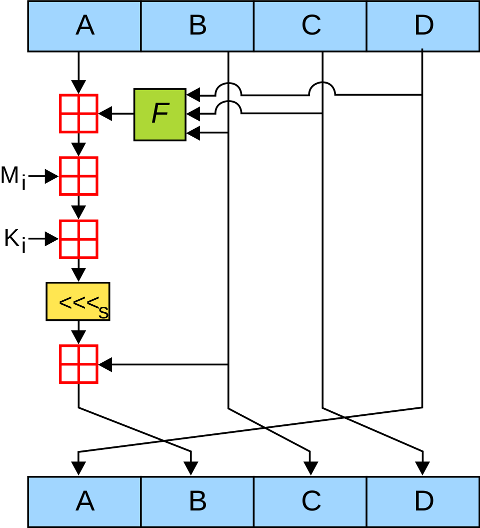
Pseudocode

The MD5 hash is calculated according to this algorithm. All values are in little-endian

Note: All variables are unsigned 32 bit and wrap modulo 2^32 when calculating
var int[64] s, K
var int i
 
//s specifies the per-round shift amounts
s[ 0..15] := { 7, 12, 17, 22,  7, 12, 17, 22,  7, 12, 17, 22,  7, 12, 17, 22 }
s[16..31] := { 5,  9, 14, 20,  5,  9, 14, 20,  5,  9, 14, 20,  5,  9, 14, 20 }
s[32..47] := { 4, 11, 16, 23,  4, 11, 16, 23,  4, 11, 16, 23,  4, 11, 16, 23 }
s[48..63] := { 6, 10, 15, 21,  6, 10, 15, 21,  6, 10, 15, 21,  6, 10, 15, 21 }
 
//Use binary integer part of the sines of integers (Radians) as constants:
for i from 0 to 63
    K[i] := floor(232 × abs(sin(i + 1)))
end for
//(Or just use the following precomputed table):
K[ 0.. 3] := { 0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee }
K[ 4.. 7] := { 0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501 }
K[ 8..11] := { 0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be }
K[12..15] := { 0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821 }
K[16..19] := { 0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa }
K[20..23] := { 0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8 }
K[24..27] := { 0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed }
K[28..31] := { 0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a }
K[32..35] := { 0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c }
K[36..39] := { 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70 }
K[40..43] := { 0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05 }
K[44..47] := { 0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665 }
K[48..51] := { 0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039 }
K[52..55] := { 0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1 }
K[56..59] := { 0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1 }
K[60..63] := { 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391 }
 
//Initialize variables:
var int a0 := 0x67452301   //A
var int b0 := 0xefcdab89   //B
var int c0 := 0x98badcfe   //C
var int d0 := 0x10325476   //D
 
//Pre-processing: adding a single 1 bit
append "1" bit to message    
// Notice: the input bytes are considered as bits strings,
//  where the first bit is the most significant bit of the byte
 
//Pre-processing: padding with zeros
append "0" bit until message length in bits ≡ 448 (mod 512)
append original length in bits mod 264 to message
 
//Process the message in successive 512-bit chunks:
for each 512-bit chunk of padded message
    break chunk into sixteen 32-bit words M[j], 0 ≤ j ≤ 15
    //Initialize hash value for this chunk:
    var int A := a0
    var int B := b0
    var int C := c0
    var int D := d0
    //Main loop:
    for i from 0 to 63
        var int F, g
        if 0 ≤ i ≤ 15 then
            F := (B and C) or ((not B) and D)
            g := i
        else if 16 ≤ i ≤ 31 then
            F := (D and B) or ((not D) and C)
            g := (5×i + 1) mod 16
        else if 32 ≤ i ≤ 47 then
            F := B xor C xor D
            g := (3×i + 5) mod 16
        else if 48 ≤ i ≤ 63 then
            F := C xor (B or (not D))
            g := (7×i) mod 16
        //Be wary of the below definitions of a,b,c,d
        F := F + A + K[i] + M[g]  //M[g] must be a 32-bits block
        A := D
        D := C
        C := B
        B := B + leftrotate(F, s[i])
    end for
    //Add this chunk's hash to result so far:
    a0 := a0 + A
    b0 := b0 + B
    c0 := c0 + C
    d0 := d0 + D
end for
 
var char digest[16] := a0 append b0 append c0 append d0 //(Output is in little-endian)
 
//leftrotate function definition
leftrotate (x, c)
    return (x << c) binary or (x >> (32-c));

Note: Instead of the formulation from the original RFC 1321 shown, the following may be used for improved efficiency useful if assembly language is being used – otherwise, the compiler will generally optimize the above code. Since each computation is dependent on another in these formulations, this is often slower than the above method where the nand/and can be parallelised):

( 0 ≤ i ≤ 15): F := D xor (B and (C xor D))
(16 ≤ i ≤ 31): F := C xor (D and (B xor C))

HMAC-SHA

HMAC-SHA1 generation

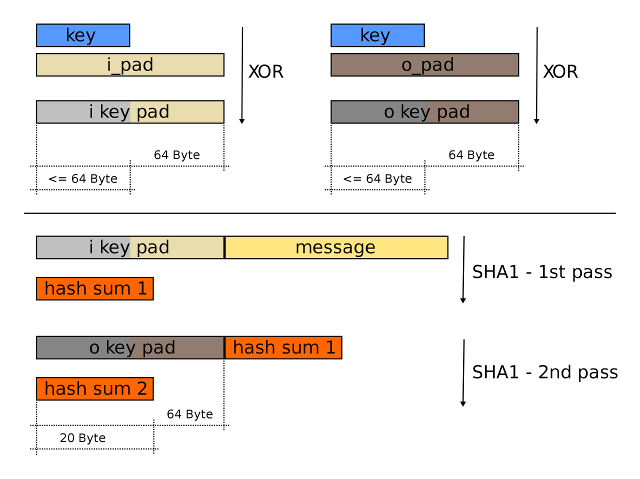
In cryptography, an HMAC (sometimes expanded as either keyed-hash message authentication code or hash-based message authentication code) is a specific type of message authentication code (MAC) involving a cryptographic hash function and a secret cryptographic key. It may be used to simultaneously verify both the data integrity and the authenticity of a message, as with any MAC. Any cryptographic hash function, such as SHA-256 or SHA-3, may be used in the calculation of an HMAC; the resulting MAC algorithm is termed HMAC-X, where X is the hash function used (e.g. HMAC-SHA256 or HMAC-SHA3). The cryptographic strength of the HMAC depends upon the cryptographic strength of the underlying hash function, the size of its hash output, and the size and quality of the key

HMAC uses two passes of hash computation. The secret key is first used to derive two keys–inner and outer. The first pass of the algorithm produces an internal hash derived from the message and the inner key. The second pass produces the final HMAC code derived from the inner hash result and the outer key. Thus the algorithm provides better immunity against length extension attacks

An iterative hash function breaks up a message into blocks of a fixed size and iterates over them with a compression function. For example, SHA-256 operates on 512-bit blocks. The size of the output of HMAC is the same as that of the underlying hash function (e.g., 256 and 1600 bits in the case of SHA-256 and SHA-3, respectively), although it can be truncated if desired

HMAC does not encrypt the message. Instead, the message (encrypted or not) must be sent alongside the HMAC hash. Parties with the secret key will hash the message again themselves, and if it is authentic, the received and computed hashes will match

The definition and analysis of the HMAC construction was first published in 1996 in a paper by Mihir Bellare, Ran Canetti, and Hugo Krawczyk,[1] and they also wrote RFC 2104 in 1997. The 1996 paper also defined a variant called NMAC. FIPS PUB 198 generalizes and standardizes the use of HMACs. HMAC is used within the IPsec and TLS protocols and for JSON Web Token

This definition is taken from RFC 2104:

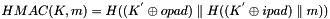
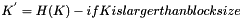
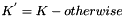
where

• H is a cryptographic hash function
• m is the message to be authenticated
• K is a secret key
• K' is a block-sized key derived from the secret key, K; either by padding to the right with 0s up to the block size, or by hashing down to less than the block size first and then padding to the right with zeros
• denotes concatenation
• denotes bitwise exclusive or (XOR)
• opad is the block-sized outer padding, consisting of repeated bytes valued 0x5c
• ipad is the block-sized inner padding, consisting of repeated bytes valued 0x36

AES-CMAC and AES-XCBC-MAC

AES-CMAC and AES-XCBC-MAC Authentication

One-key MAC (OMAC) is a message authentication code constructed from a block cipher much like the CBC-MAC algorithm. Officially there are two OMAC algorithms (OMAC1 and OMAC2) which are both essentially the same except for a small tweak. OMAC1 is equivalent to CMAC, which became an NIST recommendation in May 2005

It is free for all uses: it is not covered by any patents.[citation needed] In cryptography, CMAC (Cipher-based Message Authentication Code)[1] is a block cipher-based message authentication code algorithm. It may be used to provide assurance of the authenticity and, hence, the integrity of binary data. This mode of operation fixes security deficiencies of CBC-MAC (CBC-MAC is secure only for fixed-length messages)

The core of the CMAC algorithm is a variation of CBC-MAC that Black and Rogaway proposed and analyzed under the name XCBC and submitted to NIST. The XCBC algorithm efficiently addresses the security deficiencies of CBC-MAC, but requires three keys. Iwata and Kurosawa proposed an improvement of XCBC and named the resulting algorithm One-Key CBC-MAC (OMAC) in their papers. They later submitted OMAC1, a refinement of OMAC, and additional security analysis. The OMAC algorithm reduces the amount of key material required for XCBC. CMAC is equivalent to OMAC1

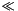
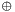
To generate an l-bit CMAC tag (t) of a message (m) using a b-bit block cipher (E) and a secret key (k), one first generates two b-bit sub-keys (k1 and k2) using the following algorithm (this is equivalent to multiplication by x and x2 in a finite field GF(2b)). Let denote the standard left-shift operator and denote bit-wise exclusive or:

1. Calculate a temporary value k0 = Ek(0)
2. If msb(k0) = 0, then k1 = k0 1, else k1 = (k0 1) C; where C is a certain constant that depends only on b. (Specifically, C is the non-leading coefficients of the lexicographically first irreducible degree-b binary polynomial with the minimal number of ones: 0x1B for 64-bit, 0x87 for 128-bit, and 0x425 for 256-bit blocks)
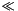
3. If msb(k1) = 0, then k2 = k1 1, else k2 = (k1 1) C
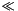
4. Return keys (k1, k2) for the MAC generation process

As a small example, suppose b = 4, C = 00112, and k0 = Ek(0) = 01012. Then k1 = 10102 and k2 = 0100 ⊕ 0011 = 01112.

The CMAC tag generation process is as follows:

1. Divide message into b-bit blocks m = m1 ... mn−1 mn, where m1, ..., mn−1 are complete blocks. (The empty message is treated as one incomplete block)
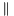
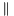
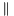
2. If mn is a complete block then mn' = k1 mn else mn' = k2 (mn
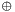
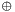
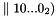
3. Let c0 = 00...02
4. For i = 1,..., n−1, calculate
5. 
6. 

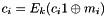
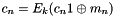
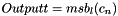
The verification process is as follows:

1. Use the above algorithm to generate the tag
2. Check that the generated tag is equal to the received tag

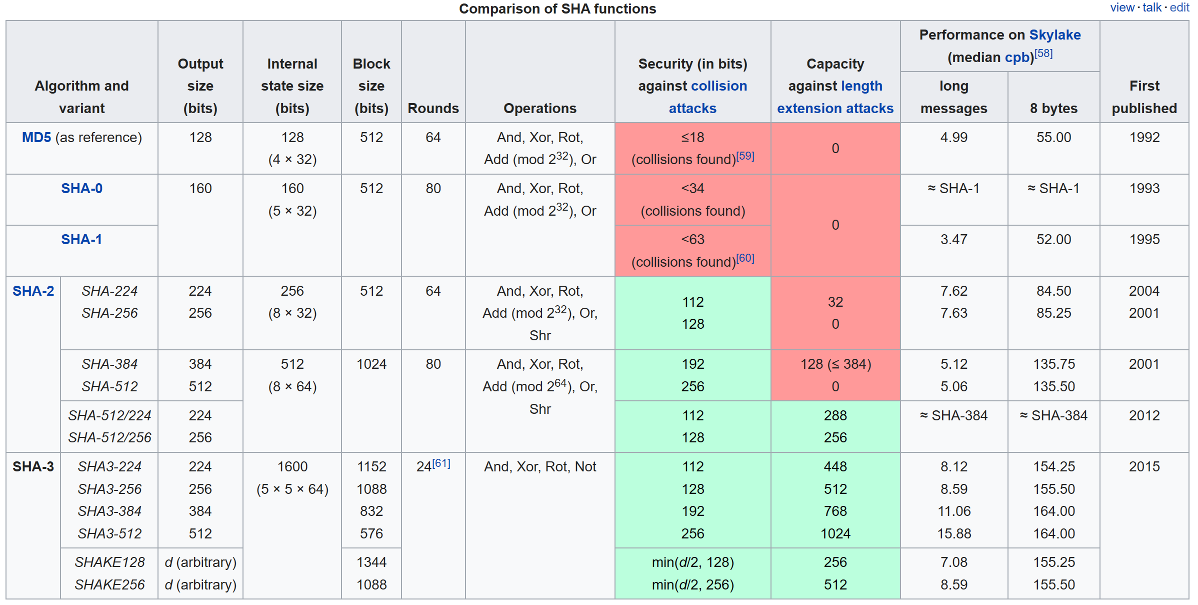
SHA3-KECCAK

Secure Hash Algorithm 3 (SHA3) is the latest member of the Secure Hash Algorithm family of standards, released by NIST on August 5, 2015. Although part of the same series of standards, SHA-3 is internally different from the MD5-like structure of SHA-1 and SHA-2.

SHA-3 is a subset of the broader cryptographic primitive family Keccak (/ˈkɛtʃæk, -ɑːk/),[6][7] designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche, building upon RadioGatún. Keccak's authors have proposed additional uses for the function, not (yet) standardized by NIST, including a stream cipher, an authenticated encryption system, a "tree" hashing scheme for faster hashing on certain architectures, and AEAD ciphers Keyak and Ketje

Keccak is based on a novel approach called sponge construction. Sponge construction is based on a wide random function or random permutation, and allows inputting ("absorbing" in sponge terminology) any amount of data, and outputting ("squeezing") any amount of data, while acting as a pseudorandom function with regard to all previous inputs. This leads to great flexibility

NIST does not currently plan to withdraw SHA-2 or remove it from the revised Secure Hash Standard. The purpose of SHA-3 is that it can be directly substituted for SHA-2 in current applications if necessary, and to significantly improve the robustness of NIST's overall hash algorithm toolkit

The creators of the Keccak algorithms and the SHA-3 functions suggest using the faster function KangarooTwelve with adjusted parameters and a new tree hashing mode without extra overhead for small message sizes

Design

The sponge construction for hash functions. Pi are input, Zi are hashed output. The unused "capacity" c should be twice the desired resistance to collision or preimage attacks

SHA-3 uses the sponge construction, in which data is "absorbed" into the sponge, then the result is "squeezed" out. In the absorbing phase, message blocks are XORed into a subset of the state, which is then transformed as a whole using a permutation function f. In the "squeeze" phase, output blocks are read from the same subset of the state, alternated with the state transformation function f. The size of the part of the state that is written and read is called the "rate" (denoted r), and the size of the part that is untouched by input/output is called the "capacity" (denoted c). The capacity determines the security of the scheme. The maximum security level is half the capacity

Given an input bit string N, a padding function pad, a permutation function f that operates on bit blocks of width b, a rate r and an output length d, we have capacity c = b − r and the sponge construction Z = sponge[f,pad,r](N,d), yielding a bit string Z of length d, works as follows:

• pad the input N using the pad function, yielding a padded bit string P with a length divisible by r (such that n = len(P)/r is integer)
• break P into n consecutive r-bit pieces P0, ..., Pn−1
• initialize the state S to a string of b zero bits
• absorb the input into the state: for each block Pi:
  • extend Pi at the end by a string of c zero bits, yielding one of length b
  • XOR that with S
  • apply the block permutation f to the result, yielding a new state S
• initialize Z to be the empty string
• while the length of Z is less than d:
  • append the first r bits of S to Z
  • if Z is still less than d bits long, apply f to S, yielding a new state S
• truncate Z to d bits

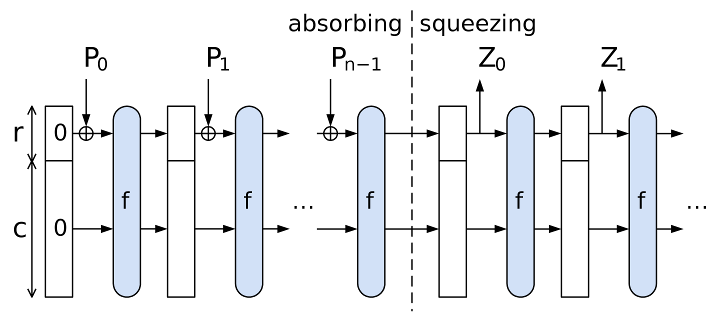
The fact that the internal state S contains c additional bits of information in addition to what is output to Z prevents the length extension attacks that SHA-2, SHA-1, MD5 and other hashes based on the Merkle–Damgård construction are susceptible to

In SHA-3, the state S consists of a 5 × 5 array of w-bit words (with w=64), b = 5 × 5 × w = 5 × 5 × 64 = 1600 bits total. Keccak is also defined for smaller power-of-2 word sizes w down to 1 bit (total state of 25 bits). Small state sizes can be used to test cryptanalytic attacks, and intermediate state sizes (from w = 8, 200 bits, to w = 32, 800 bits) can be used in practical, lightweight applications

For SHA-3-224, SHA-3-256, SHA-3-384, and SHA-3-512 instances, r is greater than d, so there is no need for additional block permutations in the squeezing phase; the leading d bits of the state are the desired hash. However, SHAKE-128 and SHAKE-256 allow an arbitrary output length, which is useful in applications such as optimal asymmetric encryption padding

Padding

To ensure the message can be evenly divided into r-bit blocks, padding is required. SHA-3 uses the pattern 10*1 in its padding function: a 1 bit, followed by zero or more 0 bits (maximum r − 1) and a final 1 bit

The maximum of r − 1 zero bits occurs when the last message block is r − 1 bits long. Then another block is added after the initial 1 bit, containing r − 1 zero bits before the final 1 bit

The two 1 bits will be added even if the length of the message is already divisible by r.[24]:5.1 In this case, another block is added to the message, containing a 1 bit, followed by a block of r − 2 zero bits and another 1 bit. This is necessary so that a message with length divisible by r ending in something that looks like padding does not produce the same hash as the message with those bits removed

The initial 1 bit is required so messages differing only in a few additional 0 bits at the end do not produce the same hash

The position of the final 1 bit indicates which rate r was used (multi-rate padding), which is required for the security proof to work for different hash variants. Without it, different hash variants of the same short message would be the same up to truncation

Poly1305-AES

Poly1305 is a cryptographic message authentication code (MAC) created by Daniel J. Bernstein. It can be used to verify the data integrity and the authenticity of a message. A variant of Bernstein's Poly1305 that does not require AES has been standardized by the Internet Engineering Task Force in RFC 8439

The original proposal, Poly1305-AES, which uses AES block cipher to expand key, computes a 128-bit (16 bytes) authenticator of a variable-length message, using a 128-bit AES key, a 128-bit additional key (with 106 effective key bits), r, and a 128-bit nonce. The message is broken into 16-byte chunks which become coefficients of a polynomial in r, evaluated modulo the prime number 2130−5. The name is derived from this and the use of 2130−5 and the Advanced Encryption Standard. In NaCl Poly1305 is used with Salsa20 instead of AES, in TLS and SSH it is used with ChaCha20 keystream

Google has selected Poly1305 along with Bernstein's ChaCha20 symmetric cipher as a replacement for RC4 in TLS/SSL, which is used for Internet security. Google's initial implementation is used in securing https (TLS/SSL) traffic between the Chrome browser on Android phones and Google's websites. Use of ChaCha20/Poly1305 has been standardized in RFC 7905

Shortly after Google's adoption for use in TLS, both ChaCha20 and Poly1305 support was added to OpenSSH via the chach.nosp@m.a20-.nosp@m.poly1.nosp@m.305@.nosp@m.opens.nosp@m.sh.c.nosp@m.om authenticated encryption cipher. Subsequently, this made it possible for OpenSSH to remove its dependency on OpenSSL through a compile-time option

Security

The security of Poly1305-AES is very close to the underlying AES block cipher algorithm. Consequently, the only way for an attacker to break Poly1305-AES is to break AES

For instance, assuming that messages are packets up to 1024 bytes; that the attacker sees 264 messages authenticated under a Poly1305-AES key; that the attacker attempts a whopping 275 forgeries; and that the attacker cannot break AES with probability above δ; then, with probability at least 0.999999-δ, all the 275 are rejected

Speed

Poly1305-AES can be computed at high speed in various CPUs: for an n-byte message, no more than 3.1n+780 Athlon cycles are needed, for example. The author has released optimized source code for Athlon, Pentium Pro/II/III/M, PowerPC, and UltraSPARC, in addition to non-optimized reference implementations in C and C++ as public domain software

Cycle Redundency Check (CRC)

A cyclic redundancy check (CRC) is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to raw data. Blocks of data entering these systems get a short check value attached, based on the remainder of a polynomial division of their contents. On retrieval, the calculation is repeated and, in the event the check values do not match, corrective action can be taken against data corruption. CRCs can be used for error correction (see bitfilters)

CRCs are so called because the check (data verification) value is a redundancy (it expands the message without adding information) and the algorithm is based on cyclic codes. CRCs are popular because they are simple to implement in binary hardware, easy to analyze mathematically, and particularly good at detecting common errors caused by noise in transmission channels. Because the check value has a fixed length, the function that generates it is occasionally used as a hash function

The CRC was invented by W. Wesley Peterson in 1961; the 32-bit CRC function, used in Ethernet and many other standards, is the work of several researchers and was published in 1975

CRCs are based on the theory of cyclic error-correcting codes. The use of systematic cyclic codes, which encode messages by adding a fixed-length check value, for the purpose of error detection in communication networks, was first proposed by W. Wesley Peterson in 1961. Cyclic codes are not only simple to implement but have the benefit of being particularly well suited for the detection of burst errors: contiguous sequences of erroneous data symbols in messages. This is important because burst errors are common transmission errors in many communication channels, including magnetic and optical storage devices. Typically an n-bit CRC applied to a data block of arbitrary length will detect any single error burst not longer than n bits, and the fraction of all longer error bursts that it will detect is (1 − 2−n)

Specification of a CRC code requires definition of a so-called generator polynomial. This polynomial becomes the divisor in a polynomial long division, which takes the message as the dividend and in which the quotient is discarded and the remainder becomes the result. The important caveat is that the polynomial coefficients are calculated according to the arithmetic of a finite field, so the addition operation can always be performed bitwise-parallel (there is no carry between digits)

In practice, all commonly used CRCs employ the Galois field of two elements, GF(2). The two elements are usually called 0 and 1, comfortably matching computer architecture

A CRC is called an n-bit CRC when its check value is n bits long. For a given n, multiple CRCs are possible, each with a different polynomial. Such a polynomial has highest degree n, which means it has n + 1 terms. In other words, the polynomial has a length of n + 1; its encoding requires n + 1 bits. Note that most polynomial specifications either drop the MSB or LSB, since they are always 1. The CRC and associated polynomial typically have a name of the form CRC-n-XXX as in the table below

The simplest error-detection system, the parity bit, is in fact a 1-bit CRC: it uses the generator polynomial x + 1 (two terms), and has the name CRC-1

Data Integrity

CRCs are specifically designed to protect against common types of errors on communication channels, where they can provide quick and reasonable assurance of the integrity of messages delivered. However, they are not suitable for protecting against intentional alteration of data

Firstly, as there is no authentication, an attacker can edit a message and recompute the CRC without the substitution being detected. When stored alongside the data, CRCs and cryptographic hash functions by themselves do not protect against intentional modification of data. Any application that requires protection against such attacks must use cryptographic authentication mechanisms, such as message authentication codes or digital signatures (which are commonly based on cryptographic hash functions)

Secondly, unlike cryptographic hash functions, CRC is an easily reversible function, which makes it unsuitable for use in digital signatures

Thirdly, CRC is a linear function with a property that

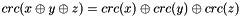
as a result, even if the CRC is encrypted with a stream cipher that uses XOR as its combining operation (or mode of block cipher which effectively turns it into a stream cipher, such as OFB or CFB), both the message and the associated CRC can be manipulated without knowledge of the encryption key; this was one of the well-known design flaws of the Wired Equivalent Privacy (WEP) protocol

SM3 Hash Algorithm

See https://tools.ietf.org/id/draft-oscca-cfrg-sm3-02.html for more information

SM3 is a cryptographic hash function used in the Chinese National Standard. It was published by the State Cryptography Administration (Chinese: 国家密码管理局) on 2010-12-17[1][2] as "GM/T 0004-2012: SM3 cryptographic hash algorithm"

SM3 is mainly used in digital signatures, message authentication codes, and pseudorandom number generators. The algorithm is public and is claimed by the China Internet Network Information Center to be like SHA-256 in security and efficiency

Introduction

The algorithm described in this document is published ([SM3]) by the Chinese Commercial Cryptography Administration Office. This document gives IETF standard description of these algorithms and parameters

Algorithm

This chatper introduces the algorithm itself. The content and structure strictly follows what is published by the Chinese Commercial Cryptography Administration Office

Scope of SM3

This document defines SM3 Hash algorithms and gives computing examples. It can be used in commercial cryptography applicaitons like digital signature and verification, message authentication code and verification, and random number generation. This document can also be a technical reference of security product and standards in order to improve the trustworthiness and interoperability of standards

Definitions and Terms

• Bit String - String composed of 0 and 1
• Big-endian - A format that describes the order in which data is stored in computer memory. It defines that the bytes with most significant value are stored at the left and bytes with least significant value are stored at the right. The high digits of a number are stored at high storage address and the low digits of a number are stored at low storage address
• Message - Bit string with arbitary length. In this document a message is consider the input of the hash algorithm
• Hash Value - The bit string which is the output after the hash algorithm applied to a message. The length of the hash value in this document is 256 bits
• Word - A bit string with length 32

Iteration Procedure

The procedure is:

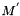
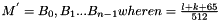
Divide the message after padding into 512 bit blocks:

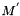
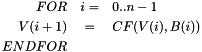
Apply iteration operation to as follows:

where CF is the compression function, V(0) is a 256 bit of IV[not], B(i) is a message block after padding, and the result after iterative compression is V(n)

Message Extension

Divide the message block B(i) into 32-bit words, then apply the words into the compression function:

a) divide message block B(i) into 16 words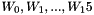

b)

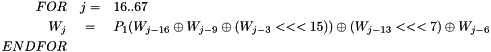
c)

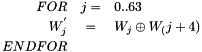
Compression function

• Let A,B,C,D,E,F,G,H be registers to store words
• Let SS1, SS2, TT1 and TT2 be intermediate variables

The compression function is as follows:

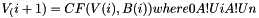
The computation precedure is as follows:

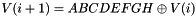
where a word is stored in memory as big-endian format

Hash Value

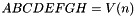
The 256 bits of the hash value is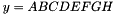

For API Documentation:

See also

ProtocolPP::jintegritysa

ProtocolPP::jsnow3g

ProtocolPP::jzuc

For Additional Documentation:

See also

jintegrity

jintegritysa

jsnow3g

jzuc

Protocol++® (ProtocolPP®) written by : John Peter Greninger • © John Peter Greninger 2015-2024 • All Rights Reserved _{All copyrights and trademarks are the property of their respective owners}

The source code contained or described herein and all documents related to the source code (herein called "Material") are owned by John Peter Greninger and Sheila Rocha Greninger. Title to the Material remains with John Peter Greninger and Sheila Rocha Greninger. The Material contains trade secrets and proprietary and confidential information of John Peter Greninger and Sheila Rocha Greninger. The Material is protected by worldwide copyright and trade secret laws and treaty provisions. No part of the Material may be used, copied, reproduced, modified, published, uploaded, posted, transmitted, distributed, or disclosed in any way without prior express written consent of John Peter Greninger and Sheila Rocha Greninger (both are required)

No license under any patent, copyright, trade secret, or other intellectual property right is granted to or conferred upon you by disclosure or delivery of the Materials, either expressly, by implication, inducement, estoppel, or otherwise. Any license under such intellectual property rights must be express and approved by John Peter Greninger and Sheila Rocha Greninger in writing

Licensing information can be found at www.protocolpp.com/license with use of the binary forms permitted provided that the following conditions are met:

• Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution
• Any and all modifications must be returned to John Peter Greninger at GitHub.com https://github.com/jpgreninger/protocolpp for evaluation. Inclusion of modifications in the source code shall be determined solely by John Peter Greninger. Failure to provide modifications shall render this license NULL and VOID and revoke any rights to use of Protocol++®
• Commercial use (incidental or not) requires a fee-based license obtainable at www.protocolpp.com/shop
• Academic or research use requires prior written and notarized permission from John Peter and Sheila Rocha Greninger

Use of the source code requires purchase of the source code. Source code can be purchased at www.protocolpp.com/shop

• US Copyrights at https://www.copyright.gov/
  • TXu002059872 (Version 1.0.0)
  • TXu002066632 (Version 1.2.7)
  • TXu002082674 (Version 1.4.0)
  • TXu002097880 (Version 2.0.0)
  • TXu002169236 (Version 3.0.1)
  • TXu002182417 (Version 4.0.0)
  • TXu002219402 (Version 5.0.0)
  • TXu002272076 (Version 5.2.1)
  • TXu002383571 (Version 5.4.3)

The name of its contributor may not be used to endorse or promote products derived from this software without specific prior written permission and licensing

THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDER AND CONTRIBUTOR "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE

---

The documentation for this class was generated from the following file:

• include/jintegritysa.h