#include "include/jecdsaf2msa.h"
Detailed Description
Elliptic Curve Digital Signature Algorithm Security Association (ECF2MDSASA) for F2M
see https://en.wikipedia.org/wiki/Elliptic_Curve_Digital_Signature_Algorithm
In cryptography, the Elliptic Curve Digital Signature Algorithm (ECDSA) offers a variant of the Digital Signature Algorithm (DSA) which uses elliptic curve cryptography
Key and signature-size comparison to DSA
As with elliptic-curve cryptography in general, the bit size of the public key believed to be needed for ECDSA is about twice the size of the security level, in bits. For example, at a security level of 80 bits (meaning an attacker requires a maximum of about 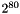
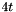
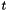
Signature generation algorithm
Suppose Alice wants to send a signed message to Bob. Initially, they must agree on the curve parameters ( CURVE , G , n ). In addition to the field and equation of the curve, we need G, a base point of prime order on the curve; n is the multiplicative order of the point G
| Parameter | Description |
|---|---|
| CURVE | the elliptic curve field and equation used |
| G | elliptic curve base point, such as a pt 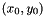 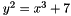 |
| n | integer order of 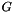 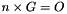 |
The order n of the base point G must be prime. Indeed, we assume that every nonzero element of the ring 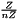
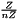
Alice creates a key pair, consisting of a private key integer 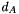
![$ [ 1 , n - 1 ]$](form_277.png)
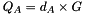
We use 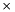
For Alice to sign a message m, she follows these steps:
- Calculate
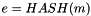
- Let
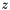
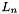
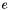
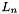
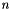
- Select a cryptographically secure random integer k from
![$ [1 , n - 1]$](form_286.png)
- Calculate the curve point
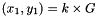
- Calculate
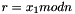
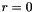
- Calculate
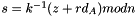
- If
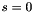
- The signature is the pair
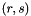
When computing 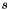
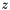
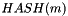
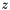
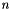
As the standard notes, it is not only required for k to be secret, but it is also crucial to select different k for different signatures, otherwise the equation in step 6 can be solved for 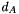
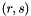
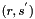
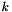
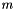
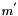
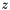
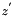
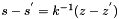
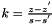
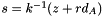
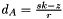
Another way ECDSA signature may leak private keys is when k is generated by a faulty random number generator. To ensure that k is unique for each message one may bypass random number generation completely and generate deterministic signatures by deriving k from both the message and the private key
Signature verification algorithm
For Bob to authenticate Alice's signature, he must have a copy of her public-key curve point 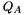
Bob can verify 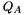
- Check that
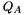
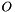
- Check that
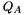
- Check that
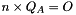
After that, Bob follows these steps:
- Verify that
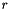
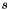
![$ [1, n - 1]$](form_305.png)
- Calculate
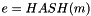
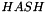
- Let
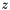
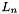
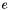
- Calculate
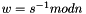
- Calculate
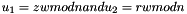
- Calculate the curve point
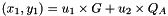
- If
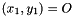
- The signature is valid if
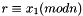
Note that using Shamir's trick, a sum of two scalar multiplications 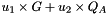
Concerns
There exist two sorts of concerns with ECDSA:
- Political concerns: the trustworthiness of NIST-produced curves being questioned after revelations that the NSA willingly inserts backdoors into software, hardware components and published standards were made; well-known cryptographers have expressed doubts about how the NIST curves were designed, and voluntary tainting has already been proved in the past
- Technical concerns: the difficulty of properly implementing the standard, its slowness, and design flaws which reduce security in insufficiently defensive implementations of the Dual EC DRBG random number generator
For API information:
- See also
- ProtocolPP::jsecass
- ProtocolPP::jecdsaf2msa
- ProtocolPP::jecdsaf2m
- ProtocolPP::jprotocol
- ProtocolPP::jprotocolpp
- ProtocolPP::jenum
For Additional Documentation:
- See also
- jsecass
- jecdsaf2msa
- jecdsaf2m
- jprotocol
- jprotocolpp
- jenum
The source code contained or described herein and all documents related to the source code (herein called "Material") are owned by John Peter Greninger and Sheila Rocha Greninger. Title to the Material remains with John Peter Greninger and Sheila Rocha Greninger. The Material contains trade secrets and proprietary and confidential information of John Peter Greninger and Sheila Rocha Greninger. The Material is protected by worldwide copyright and trade secret laws and treaty provisions. No part of the Material may be used, copied, reproduced, modified, published, uploaded, posted, transmitted, distributed, or disclosed in any way without prior express written consent of John Peter Greninger and Sheila Rocha Greninger (both are required)
No license under any patent, copyright, trade secret, or other intellectual property right is granted to or conferred upon you by disclosure or delivery of the Materials, either expressly, by implication, inducement, estoppel, or otherwise. Any license under such intellectual property rights must be express and approved by John Peter Greninger and Sheila Rocha Greninger in writing
Licensing information can be found at www.protocolpp.com/license with use of the binary forms permitted provided that the following conditions are met:
- Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution
- Any and all modifications must be returned to John Peter Greninger at GitHub.com https://github.com/jpgreninger/protocolpp for evaluation. Inclusion of modifications in the source code shall be determined solely by John Peter Greninger. Failure to provide modifications shall render this license NULL and VOID and revoke any rights to use of Protocol++®
- Commercial use (incidental or not) requires a fee-based license obtainable at www.protocolpp.com/shop
- Academic or research use requires prior written and notarized permission from John Peter and Sheila Rocha Greninger
Use of the source code requires purchase of the source code. Source code can be purchased at www.protocolpp.com/shop
- US Copyrights at https://www.copyright.gov/
- TXu002059872 (Version 1.0.0)
- TXu002066632 (Version 1.2.7)
- TXu002082674 (Version 1.4.0)
- TXu002097880 (Version 2.0.0)
- TXu002169236 (Version 3.0.1)
- TXu002182417 (Version 4.0.0)
- TXu002219402 (Version 5.0.0)
- TXu002272076 (Version 5.2.1)
- TXu002383571 (Version 5.4.3)
The name of its contributor may not be used to endorse or promote products derived from this software without specific prior written permission and licensing
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDER AND CONTRIBUTOR "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE
The documentation for this class was generated from the following file:
- include/jecdsaf2msa.h