#include "include/jdsa.h"
Detailed Description
Digital Signature Algorithm
see https://en.wikipedia.org/wiki/Digital_Signature_Algorithm
The Digital Signature Algorithm (DSA) is a Federal Information Processing Standard for digital signatures, based on the mathematical concept of modular exponentiations and the discrete logarithm problem.
In August 1991 the National Institute of Standards and Technology (NIST) proposed DSA for use in their Digital Signature Standard (DSS) and adopted it as FIPS 186 in 1994. Four revisions to the initial specification have been released: FIPS 186-1 in 1996, FIPS 186-2 in 2000, FIPS 186-3 in 2009, and FIPS 186-4 in 2013
DSA: How does it work?
The DSA algorithm works in the framework of public-key cryptosystems and is based on the algebraic properties of the modular exponentiations, together with the discrete logarithm problem (which is considered to be computationally intractable). Messages are signed by the signer's private key and the signatures are verified by the signer's corresponding public key. The digital signature provides message authentication, integrity and non-repudiation
Key generation
Key generation has two phases. The first phase is a choice of algorithm parameters which may be shared between different users of the system, while the second phase computes public and private keys for a single user
Parameter generation
Choose an approved cryptographic hash function H. In the original DSS, H was always SHA-1, but the stronger SHA-2 hash functions are approved for use in the current DSS. The hash output may be truncated to the size of a key pair
Decide on a key length L and N (the cryptographic strength of the L bit long key). The original DSS constrained L to be a multiple of 64 between 512 and 1,024 (inclusive). NIST 800-57 recommends lengths of 2,048 (or 3,072) for keys with security lifetimes extending beyond 2010 (or 2030), using correspondingly longer N. FIPS 186-3 specifies L and N length pairs of (1,024, 160), (2,048, 224), (2,048, 256), and (3,072, 256). N must be less than or equal to the output length of the hash H
Choose an 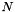
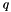
Choose an 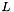
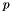
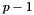
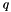
Choose g, a number whose multiplicative order modulo p is q. This means that q is the smallest positive integer such that gq=1 mod p. This may be done by setting 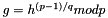
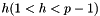
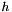
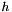
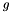
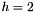
The algorithm parameters 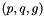
Per-user keys
Given a set of parameters, the second phase computes private and public keys for a single user:
- Choose a secret private key
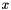
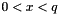
- Calculate the public key
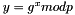
There exist efficient algorithms for computing the modular exponentiations 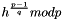
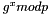
Signing
- Let H be the hashing function and m the message:
- Generate a random per-message value
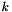
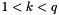
- Calculate
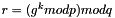
- In the unlikely case that
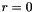
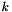
- Calculate
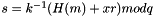
- In the unlikely case that
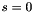
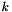
- The signature is
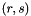
The first two steps amount to creating a new per-message key. The modular exponentiation here is the most computationally expensive part of the signing operation, and it may be computed before the message hash is known. The modular inverse
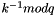
is the second most expensive part, and it may also be computed before the message hash is known. It may be computed using the extended Euclidean algorithm or using Fermat's little theorem as
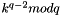
Verifying
- Reject the signature if
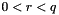
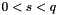
- Calculate
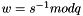
- Calculate
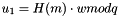
- Calculate
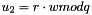
- Calculate
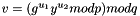
- The signature is valid if and only if
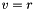
For API information:
- See also
- ProtocolPP::jdsa
- ProtocolPP::jprotocol
- ProtocolPP::jprotocolpp
- ProtocolPP::jenum
For Additional Documentation:
- See also
- jdsa
- jprotocol
- jprotocolpp
- jenum
The source code contained or described herein and all documents related to the source code (herein called "Material") are owned by John Peter Greninger and Sheila Rocha Greninger. Title to the Material remains with John Peter Greninger and Sheila Rocha Greninger. The Material contains trade secrets and proprietary and confidential information of John Peter Greninger and Sheila Rocha Greninger. The Material is protected by worldwide copyright and trade secret laws and treaty provisions. No part of the Material may be used, copied, reproduced, modified, published, uploaded, posted, transmitted, distributed, or disclosed in any way without prior express written consent of John Peter Greninger and Sheila Rocha Greninger (both are required)
No license under any patent, copyright, trade secret, or other intellectual property right is granted to or conferred upon you by disclosure or delivery of the Materials, either expressly, by implication, inducement, estoppel, or otherwise. Any license under such intellectual property rights must be express and approved by John Peter Greninger and Sheila Rocha Greninger in writing
Licensing information can be found at www.protocolpp.com/license with use of the binary forms permitted provided that the following conditions are met:
- Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution
- Any and all modifications must be returned to John Peter Greninger at GitHub.com https://github.com/jpgreninger/protocolpp for evaluation. Inclusion of modifications in the source code shall be determined solely by John Peter Greninger. Failure to provide modifications shall render this license NULL and VOID and revoke any rights to use of Protocol++®
- Commercial use (incidental or not) requires a fee-based license obtainable at www.protocolpp.com/shop
- Academic or research use requires prior written and notarized permission from John Peter and Sheila Rocha Greninger
Use of the source code requires purchase of the source code. Source code can be purchased at www.protocolpp.com/shop
- US Copyrights at https://www.copyright.gov/
- TXu002059872 (Version 1.0.0)
- TXu002066632 (Version 1.2.7)
- TXu002082674 (Version 1.4.0)
- TXu002097880 (Version 2.0.0)
- TXu002169236 (Version 3.0.1)
- TXu002182417 (Version 4.0.0)
- TXu002219402 (Version 5.0.0)
- TXu002272076 (Version 5.2.1)
- TXu002383571 (Version 5.4.3)
The name of its contributor may not be used to endorse or promote products derived from this software without specific prior written permission and licensing
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDER AND CONTRIBUTOR "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE
The documentation for this class was generated from the following file:
- include/jdsa.h